
Trong toán học, lý thuyết Ramsey đề cập tới “trật tự hỗn loạn”. Cho dù hệ thống lớn có phức tạp đến đâu thì trật tự vẫn sẽ nổi lên như một hệ thống con nhỏ hơn với cấu trúc độc đáo.
Con người từ khi có ý thức đã luôn tìm kiếm khuôn mẫu sống trong một thế giới hỗn loạn ngẫu nhiên. Chúng ta tìm kiếm trật tự trong mọi thứ, từ cuộc sống, thế giới xung quanh, đến Vũ trụ, và bạn có thể nói lý thuyết Ramsey giải thích khả năng chúng ta tìm thấy nó.
Số Ramsey có thể được coi là đại diện cho ranh giới của sự rối loạn. Và rất khó để tìm ra chúng. Kể từ khi nhà toán học Frank Ramsey chứng minh Định lý Ramsey vào cuối những năm 1920, cộng đồng toán đã có sự bối rối mà cuối cùng Sam Mattheus và Jacques Verstraete của Đại học California, San Diego đã giải được.
Verstraete nói: “Nhiều người đã nghĩ tới r(4,t) là một bài toán bỏ ngỏ trong hơn 90 năm qua. Chúng tôi thực sự đã mất nhiều năm để giải quyết. Và đã có nhiều lúc chúng tôi bế tắc và tự hỏi liệu mình có thể giải được hay không".
Một ví dụ phổ biến với lý thuyết Ramsey yêu cầu chúng ta tính xem cần mời bao nhiêu người đến một bữa tiệc sao cho có ít nhất ba người đã quen nhau hoặc ít nhất ba người sẽ hoàn toàn xa lạ với nhau.
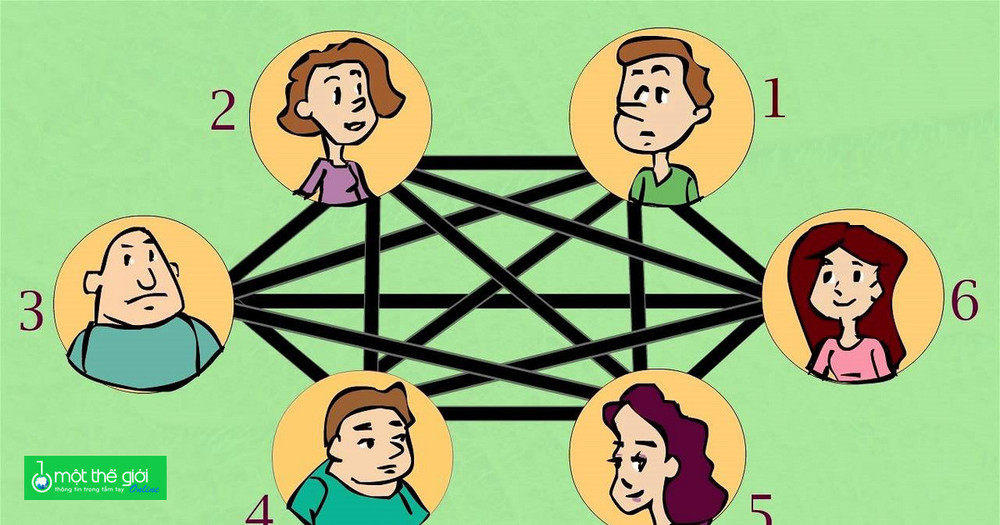
Ở đây, số Ramsey (viết tắt r), là số lượng người tối thiểu cần có trong bữa tiệc để s người biết nhau hoặc t người không biết nhau. Điều này có thể được viết dưới dạng r(s,t) và chúng ta biết đáp án r(3,3) = 6.
Video Giáo sư toán học Trefor Bazett giải thích vì sao r(3,3) lại bằng 6
Verstraete nói "Đó là sự thật hiển nhiên và... tuyệt đối. Bất kể tình huống ra sao hay bạn chọn 6 người nào thì bạn sẽ có nhóm 3 người đều biết nhau hoặc 3 người không biết nhau. Bạn có thể tìm thấy nhiều hơn, nhưng bạn được đảm bảo rằng sẽ có ít nhất 3 người trong nhóm đều biết nhau hoặc nhóm không hề biết nhau".
Các bài toán Ramsey thường được giải bằng cách sử dụng đồ thị ngẫu nhiên. Ví dụ: với s được biểu thị là những điểm có các đường màu xanh lam ở giữa chúng và t là những điểm có các đường màu đỏ. Nếu biểu đồ đủ lớn, bạn sẽ tìm thấy trật tự, nhưng nó đủ phức tạp để làm bạn rối mắt như hình bên dưới.

Các nhà toán học đã chứng minh một định lý vào những năm 1930 mà sau này chỉ ra rằng đáp số của r(4, 4) là 18. Và kể từ năm 1995, chúng ta đã biết r(4,5) = 25. Chúng ta không chắc liệu việc 4 người quen bắt chuyện hay tập hợp 5 người lạ để trao đổi câu chuyện có ý nghĩa gì hay không. Nhưng nếu bạn mời 25 người đến dự một bữa tiệc, lý thuyết của Ramsey cho rằng bạn có thể chắc chắn rằng một trong điều trên sẽ xảy ra.
Bỏ chuyện tiệc tùng sang một bên, việc tìm số Ramsey cho một vấn đề về cơ bản giúp tìm ra ít yếu tố nhất mà một hệ thống cần có để đảm bảo chắc chắn về một thuộc tính nhất định. Nó rất hữu ích trong khoa học máy tính và toán học để cấu trúc mạng truyền thông và tạo ra các thuật toán phát hiện gian lận, cùng nhiều điều khác.
Verstraete giải thích: “Bởi vì những con số này nổi tiếng là khó tìm nên giới toán học tìm kiếm các ước tính”, đồng thời đặt vấn đề: “Vậy làm thế nào khi chúng ta không tìm thấy đáp án chính xác mà lại tìm ra ước tính tốt nhất cho những con số Ramsey này?”
Sau khi phát hiện ra các ước tính có thể được thắt chặt bằng cách sử dụng đồ thị giả ngẫu nhiên, Verstraete và nhà toán học Dhruv Mubayi của Đại học Illinois-Chicago đã giải thành công r(3,t) vào năm 2019.
Nhưng Verstraete gặp khó khăn trong việc tạo ra một đồ thị giả ngẫu nhiên cho r(4,t), vì vậy ông và Mattheus đã giải quyết vấn đề tồn tại lâu nay bằng cách kết hợp lĩnh vực hình học hữu hạn với lý thuyết đồ thị.
Với sự kết hợp đó, các nhà nghiên cứu đã ấn định s (những người quen biết lẫn nhau) là 4 và nghiên cứu số Ramsey khi t (người lạ) tăng lên. Sau gần 1 năm và vượt qua nhiều trở ngại về toán học, họ đã tìm thấy r(4,t) gần bằng hàm bậc ba của t. Đối với một bữa tiệc có 4 người đều biết nhau hoặc t những người không biết nhau, bạn cần mời bao nhiêu.
Như các nhà nghiên cứu tuyên bố, đây là ước tính tốt nhất. Nếu bạn quan tâm, kết quả của họ có thể được biểu diễn dưới dạng toán học như sau: r(4,t) = Ω(t^3/log4t ) khi t → ∞.
Nhóm nghiên cứu tin rằng phương pháp của họ sẽ hữu ích cho các số Ramsey khác và có thể hỗ trợ việc ước tính các hàm toán học khác.
Verstraete nói: “Người ta không bao giờ nên bỏ cuộc, dù mất bao lâu đi chăng nữa. Nếu bạn thấy vấn đề đó khó khăn và bạn đang mắc kẹt thì nghĩa là đó là một vấn đề thú vị”.